Linear Classification

사람과 기린을 분류해야 하는데 Height와 Weight 변수를 가진 데이터가 주어졌을 때를 생각해보자. ex) [Height, Weight] : [183, 64], [154, 45], [420, 780], [164, 51], [380, 660] …
복잡한 알고리즘을 적용할 필요도 없이 Height가 250cm 이상이거나 Weight가 300kg 이상 등의 자기 객관적인 기준을 가지고도 확실하게 분류할 수 있는 모델을 만들어 낼 수 있다. 왜냐하면 사람과 기린의 갭은 엄청나게 크기 때문이다. 이와 같이 둘 중 하나로 분류되는 모델을 이진 분류 모델(Binary Classification Model)이라고 한다.

그렇다면 사람과 고릴라를 분류해야 한다고 생각해보자. 서부 고릴라의 경우 수컷은 160 ~ 180cm, 암컷은 150cm 까지 자라며 체중 또한 각각 140 ~ 180kg, 90kg 까지 성장한다. 그렇다. 사람과의 갭이 크지 않아 간단하게 알고리즘을 짤 수 없다. 아래의 그림을 보자.

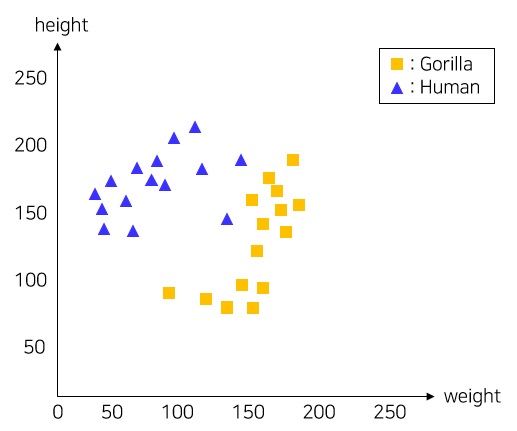
사람의 정보는 다음과 같다고 가정해보자. 세계 성인 평균 몸무게는 62kg고, 평균 신장은 165cm라고 치자. Linear Classfication 개념을 모르고 단순하게 분류한다고 가정했을 때 Height/Weight를 구해서 풀어볼 수 있을 것이다. 인간은 약 2.66이 나오며, 고릴라의 경우 1.06 ~ 1.7 까지 나온다. 인간의 경우 워낙 스펙트럼이 넓기때문에 대략 Height/Weight가 1.8 이상인 경우에 사람으로 판단한다고 하자. 즉, 기울기가 1.8인 \(y = 1.8x\) 직선의 방정식을 이용하여 데이터를 분리하는 것이다. 해당 방정식에 데이터를 대입했을 때 양수가 나오면 사람이고, 음수가 나오면 고릴라라고 판단할 수 있다. 이를 식으로 나타내보면 위의 직선의 방정식 \(y = 1.8x\)를 이항하여 \(f(x) = y - 1.8x\)의 꼴로 나타내주고, 각각의 데이터를 대입하면 된다. 이를 그림으로 나타내면 아래와 같다.

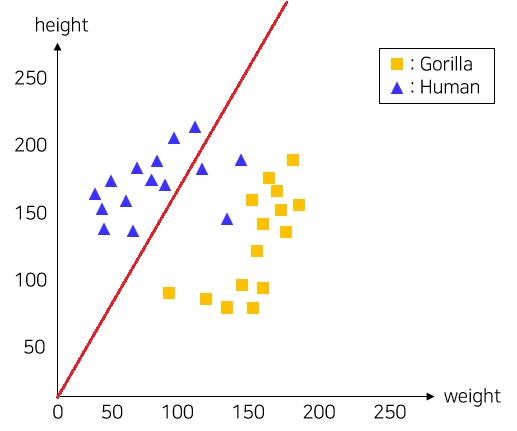
이 모델이 가장 잘 분류했다고 할 수 있을까? 해당 모델의 정확도는 전체 30개의 데이터중 3개를 틀렸기 때문에 Accuracy는 90%가 된다. 사실 이와 같은 데이터셋에서 선 하나로 잘 분류할 수 있는 경우는 아래이 30개의 데이터중 1개만을 틀리게 분류했을 경우이다. 이 때 Accuracy는 96.7%가 나온다.

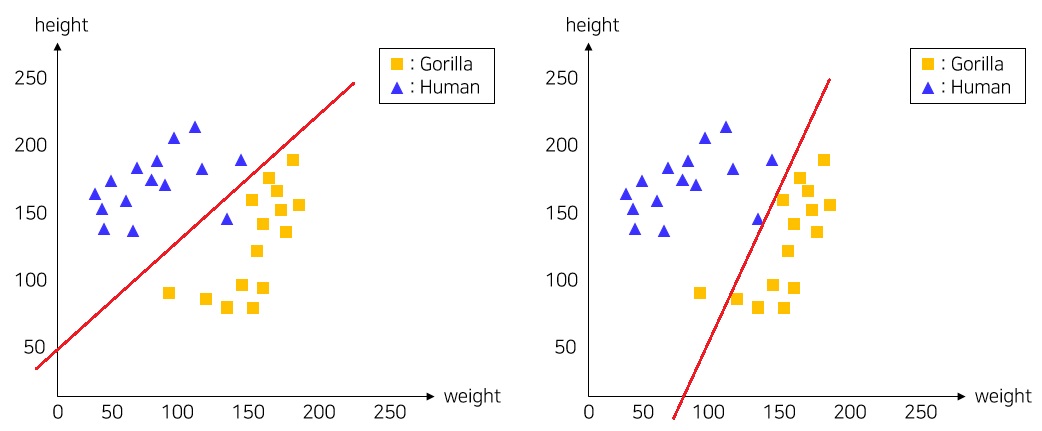
분류 모델의 성능이 좋지 않았던 이유는 직관에 의존해서 직선의 방정식을 결정했기 때문이다. 또한, 직선의 방정식 \(f(x) = ax + by + c\) 에서 a의 값만 정했을 뿐 b와 c의 값은 고려하지 않고 방정식을 구했기 때문이다. 즉, Linear Classification이란 Accuracy가 높은(혹은 Error가 낮은) 직선의 방정식(\(ax + by + c\))들을 찾아가는 과정이 Linear Classification이다.