[개념정리] Perceptron

Perceptron

본 포스트는 포스코 청년 AI Big Data 아카데미 교육과정 중 AI과정에서 POSTECH 최승진교수님(BARO CTO)의 강의를 듣고 작성했습니다.

지난번 Linear Classification에 이어 Perceptron에 대해서 다시 학습해본다. Perceptron 이란 1956년 Rosenblatt에 의해 제안된 개념으로, 1957년 Cornell Aeronautical Lab에서 개발했다고 한다. Linear Classification 을 위한 학습에 처음으로 iterative algorithm이 사용되었으며, 각 노드에서 가중치와 입력을 곱하여 합한 후 그 값이 Threshold 보다 크면 1을 취하고, Threshold 보다 작으면 0이나 -1을 취한다. 예시로, Single-layer 기반의 perceptron은 \(y = sgn(w^T x + b)\)로 나타낼 수 있다. Perceptron의 전체적인 프로세스는 아래와 같다.

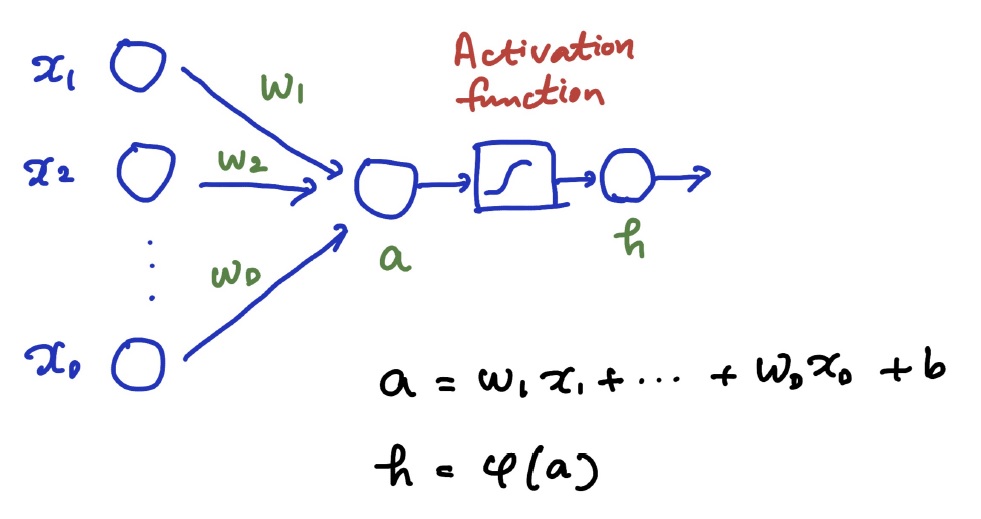
Perceptron은 On-line and mistake-driven의 procedure이다. 이 말은 즉, training 단계에서 weight의 벡터들이 분류를 잘못했을 때마다 업데이트된다는 소리이다. 또한, 데이터가 ‘Linearly separable’할 때 해당 procedure가 수렴하게 된다.(Perceptron convergence theorem에 의해) 즉, 선형으로 분리될 수 있을 때 적합한 알고리즘이다. Perceptron의 과정을 수식으로 이해해보자.
x는 input vector로 다음과 같이 나타낸다. \(x = [x_{1}, x_{2}, x_{3}, x_{4} ... x_{i}]\)
w는 weight vector로 다음과 같이 나타낸다. \(w = [w_{1}, w_{2}, w_{3}, w_{4} ... w_{i}]\)
따라서, \(g(x) = w^T x\)로 나타낼 수 있다.

Perceptron criterion

\(y_{n} = w^T x\) 일 때, Perceptron이 아래와 같이 분류할 수 있다고 가정하자.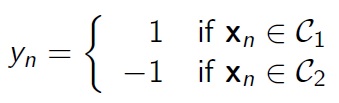
아래의 식을 만족하는 weight를 찾아가는 것이 Perceptron criterion이다.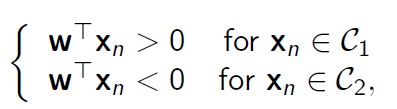

Percetpron의 학습이 어떻게 이루어지는지 자세하게 알아보자.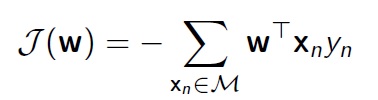
위와 같은 Objective function에 의해 Perceptron criterion이 최소화되는 방향으로 진행된다. 여기에서 M은 현재의 weight vector에 의해 잘못 분류된 데이터들을 모아놓은 set를 의미한다. Perceptron criterion이 최소화 되는 방향, 즉 J(w)의 기울기가 작아지는 방향으로 진행하게 된다.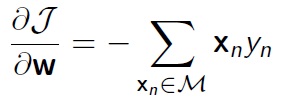
간단하게 얘기해서 \(w^{new}\) ← \(w^{old} - \alpha \frac{\partial g}{\partial w}\) 와 같이 진행된다. 여기서 \(\alpha\)는 learning rate를 의미한다. (learning rate란 학습의 속도를 조절하기 위한 변수로 알아놓자.)

즉, 정리하자면 Perceptron Learning의 알고리즘은 다음과 같다.

Get a training sample
Check to see if it is misclassified
2.1 If classified correctly, do nothing
2.2 If classified incorrectly, update w(weight) by
\(w_{k+1}=w_{k} + \alpha x_{n}y_{n}\) (gradient를 계산한 값이 -이기 때문에 +로 바뀜)
Repeat steps 1 and 2 until convergence

AI Winter

“Perceptrons : An Introduction to Computational Geometry” 라는 책에서 Minsky 와 Papert에 의해 1969년에 Perceptron은 XOR문제를 해결하지 못한다는 것을 보여 AI의 암흑기가 찾아왔다.

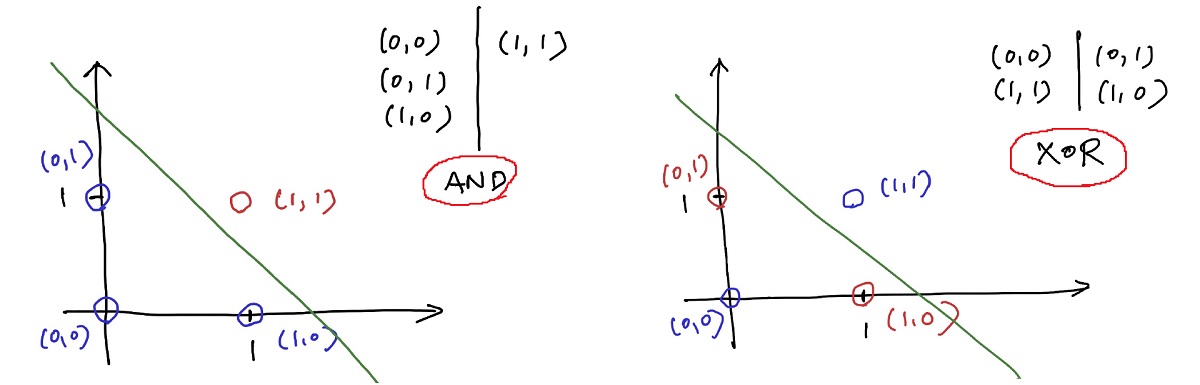
위와 같이 AND게이트의 경우 (Single)Linearly Separable 하기 때문에 Perceptron으로 분류할 수 있지만, XOR게이트의 경우 Perceptron으로 분류할 수 없다. 이는, MLP(Multi Layer Perceptron)을 통해 해결할 수 있지만, 한참 지난 1980년대에 와서야 발견되어 다시 신경망 연구가 부활하게 된다.