Bias(편향)

앞서 얘기했듯이 \(y = sgn(w^T x + b)\)로 Perceptron을 나타낼 수 있다고 했다. 여기서 \(b\)가 bias(편향)을 의미한다. 앞에서는 bias에 대해 설명하지 않고 bias를 빼고 \(g(x) = w^T x\) 로 Perceptron을 설명했지만, 오늘은 bias에 대해 공부하려고 한다.

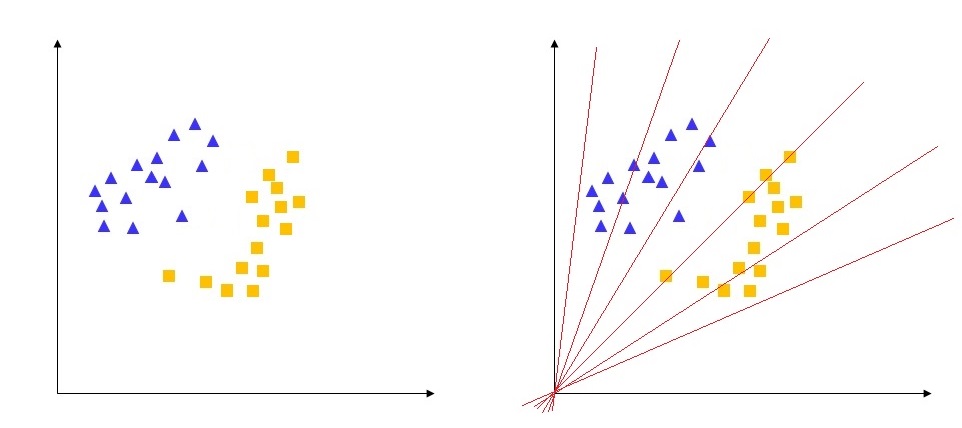
bias는 학습에서 중요한 역할을 한다. 데이터가 위의 왼쪽 그림과 같이 주어졌다고 하자. bias가 없을 때 해당 데이터를 완벽하게 분리할 수 있는가? 즉, \(g(x) = w^T x\) 로 linearly separable 한지를 생각해보면 bias가 왜 필요한지 알 수 있다.
bias가 없는 경우 단순히 input vector와 weight vector의 곱이므로 오른쪽 그림과 같이 항상 원점을 지나게 된다. 즉, 어느정도 분류를 할 수 있는 모델이 만들어지지만, 항상 원점을 지나게 되는 제약사항이 큰 비효율적인 모델을 만들게 되는 것이다.

bias를 넣어주면 위와 같이 이러한 문제점을 해결할 수 있으며, 그렇기 때문에 Perceptron의 식은 \(y = sgn(w^T x + b)\)과 같이 되는 것이다.

---

Weight(가중치)

출처 : 갈아먹는 머신러닝

weight는 신경망에서 각각의 input이 얼마나 많은 영향을 미치는지 결정하는 중요한 vector이다. 이렇게 중요한 vector들은 어떻게 Initialization 하는지에 따라 추후에 설명할 Gradient Vanishing 문제를 가지게 되거나 학습 속도에 영향을 미치는 등 모델의 성능에 영향을 끼친다. 어떠한 방식들이 사용되고 있는지 알아보자.

1. 상수 초기화

weight를 전부 0으로 초기화하면 Zeros, 1은 Ones, 임의의 상수로 초기화하면 Constant 기법이다. 임의의 값을 넣어도 오분류 시 weight가 업데이트 되기 때문에 어떤 값을 넣어도 상관없다고 생각할 수 있다. 하지만, 조금 더 생각해보면 모든 weight들이 동일한 값으로 초기화하면 학습시 모든 뉴런들이 동일한 값을 나타낸다는 얘기가 된다. 즉, backpropagation 시 각 weight들이 동일하게 업데이트가 진행될 것이기 때문에 제대로된 학습 성능을 바라기 힘들다.

2. 확률 분포 초기화

확률 분포에 의한 weight initialization은 크게 두가지로 나뉜다. Uniform distribution 방식과 Normal distribution 방식이다.

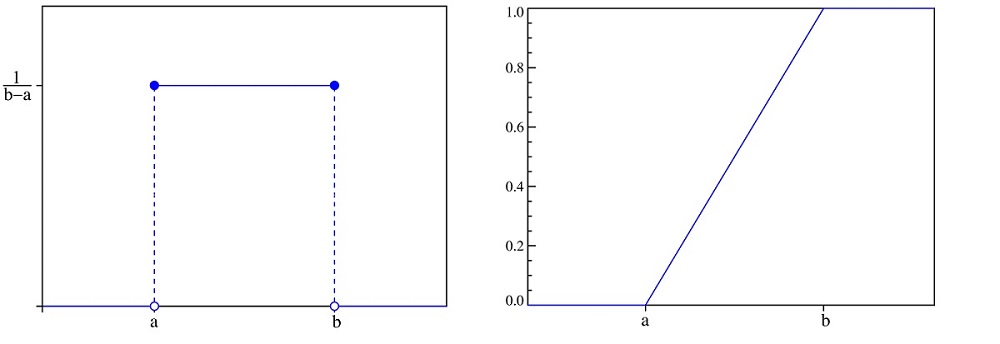
Uniform distribution 방식은 확률 밀도 함수에 의한 방식(왼쪽)과 누적 분포 함수에 의한 방식(오른쪽) 으로 나뉜다. weight 초기값이 크게 되면 Gradient Vanishing 문제나 Exploding이 발생할 수 있기 때문에 작은 값으로 초기화하는 것이 좋다.

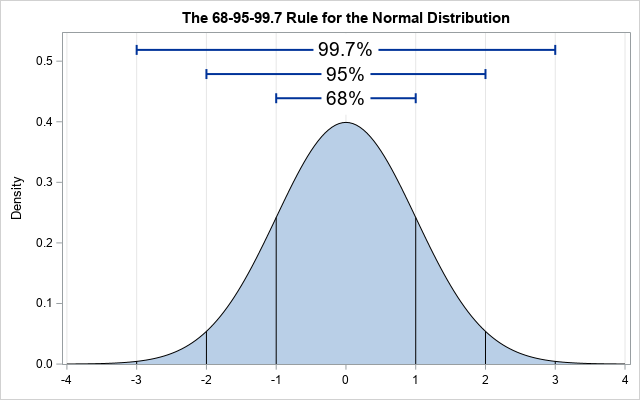
다음은 Normal distribution 방식이다. 평균에 가까울수록 확률이 높아지기 때문에 종 모양의 분포를 따르는 weight들이 생성된다. 평균과 표준편차를 어느 정도 알맞게 설정하느냐가 학습 속도에 영향을 미친다.

3. 분산 조정 초기화

실제로 현재 딥 러닝 모델에서 가장 많이 사용하는 기법이다. 확률 분포를 기반으로 weight를 초기화 하되, 확률 분포의 분산을 weight 별로 동적으로 조절하는 기법이다.

해당 기법들을 이해하려면 fan in과 fan out의 개념을 알아야한다. 우선 fan in이란 input tensor의 크기이고 fan out은 output tensor의 크기이다.

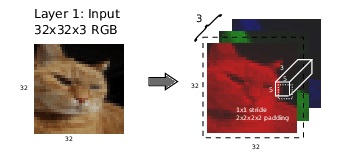
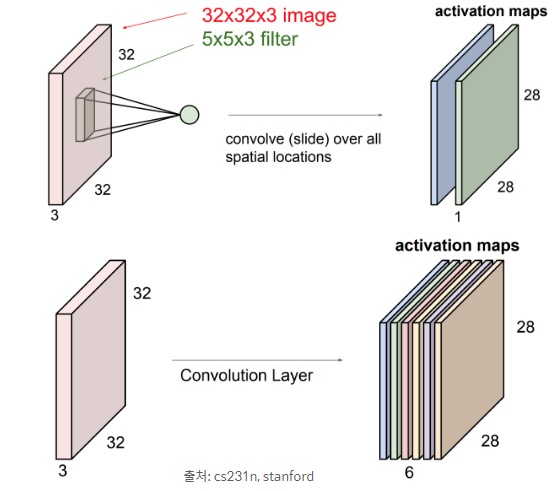
위와 같이 32(가로) x 32(세로) x 3(RGB 채널) 의 이미지를 입력받아 5 x 5 x 3 크기의 커널을 6채널 적용한 경우를 생각해보자. kernel shape = kernel size + (input channel, filters) 이기 때문에 kernel shape = (5, 5) + (3, 6) 이므로 (5, 5, 3, 6)이 된다. 이 kernel shape를 기반으로 receptive field 값을 계산한다. receptive field란 input에서 해당 kernel이 얼마나 인식하는 지를 나타낸다. 아래와 같이 해당 범위 내의 모든 값을 곱하여 나타낼 수 있다. \(receptive \, field \; = \; \displaystyle\prod_{i=0}^{k-1}kernel \, shape[i] \, = \, 5 \times 5 = 25\)

kernel shape와 receptive field를 이용해 fan in과 fan out을 계산할 수 있다.
\(fan \, in \,= \, receptive \, field \times input \, channel \, = \, 25 \times 3(kernel \, shape[k-1]) \, = \, 75\)
\(fan \, out \, = \, receptive \, field \times output \, channel \, = \, 25 \times 6(kernel \, shape[k-1]) \, = \, 150\)

Lecun Initialization

딥 러닝의 대가인 얀 리쿤 Yann Lecun