Summer/Winter Coding(2019) - 멀쩡한 사각형

• 문제 링크 : 멀쩡한 사각형

이 문제는 코드만 봐선 이해하기 어렵기 때문에 설명을 하려한다.

처음 생각했던 방법은 직선의 방정식을 구하고 x 값을 0.1 단위로 증가시켜 겹치는 행렬에 1을 넣어서 숫자를 세고 w x h에서 빼려고 했다. 구현하다보니 제한사항에 W, H가 1억 이하의 자연수라는 것을 보고 시간초과가 날 것으로 예상되어 포기했다.

그래서 규칙 찾을라고 종이에 그려보면서 발악했으나 결국 찾지 못하고 구글에 검색해서 지니어스분들의 도움을 받았다.

• 출처 : 슈퍼짱짱님의 티스토리

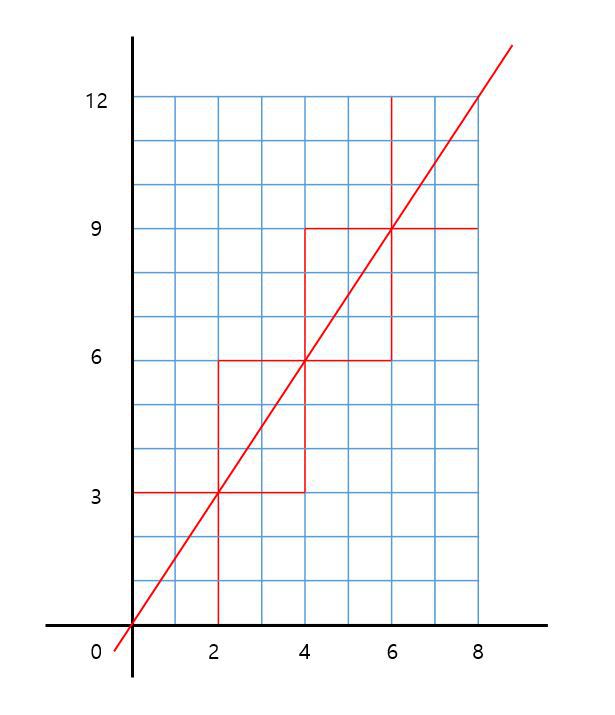
꼭짓점에서 꼭짓점을 이등분 하는 것이니 좌측 위의 꼭짓점을 기준으로 하나, 좌측 아래의 꼭짓점을 기준으로 하나 상관은 없다.

위와 같은 그림이 모눈종이에 있다고 생각해보자. 기울기는 \(y의 증가량 / x의 증가량\) 이므로 \(y = (3/2)x\)와 같다. 즉 x가 (2, 4, 6, 8)일 때 가로 격자선과 세로 격자선이 만나는 구간이므로 나누어서 생각할 수 있다. 이러한 부분이 4개가 생긴다. 왜 4개일까? 생각하고 다음의 예제도 확인해보자

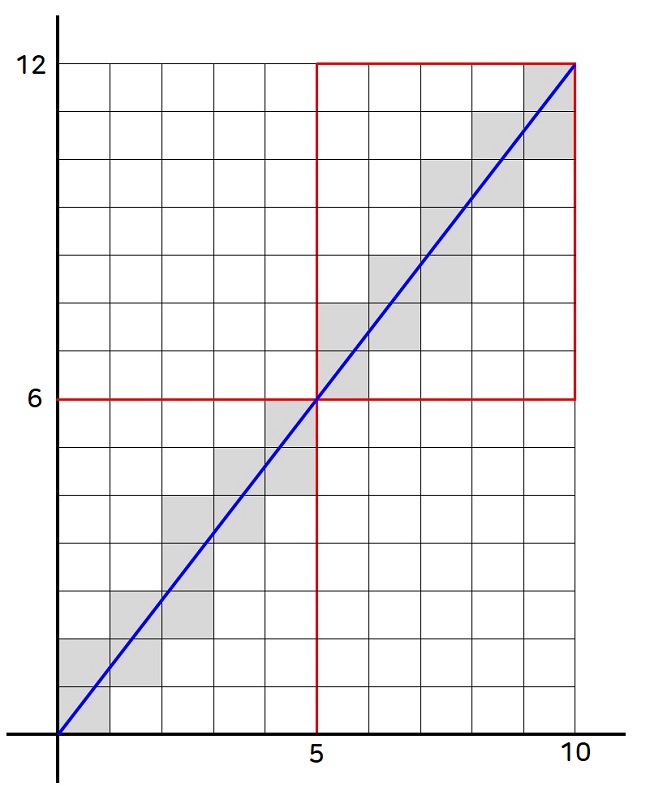
위의 그림의 기울기는 \(y의 증가량 / x의 증가량\) 이므로 \(y = (6/5)x\)와 같다. 즉 빨간색 선으로 칠한 것과 같이 2개의 부분으로 나누어서 생각할 수 있다.

두 개를 그려보니 나눌 수 있는 부분은 w, h의 최대공약수 인 것을 알 수 있다. 첫 번째 예시에서는 w(8) h(12)의 최대공약수인 4개의 부분으로 나눌 수 있었고, 두 번째 예시에서는 w(10) h(12)의 최대 공약수인 2개의 부분으로 나눌 수 있다.

나뉜 부분의 w와 h는 최대공약수인 g의 값으로 나누면 된다. 즉, 첫 번째 예시에서는 \(w = 8/4 = 2,\) \(h = 12/4 = 3\)이 된다. 즉, \(width = w/g\), \(height = h/g\)로 생각할 수 있다.

이제 나누어진 경우를 생각해보자. 사실 다양한 방식으로 그려도 정사각형의 개수는 아래와 같이 width + height - 1개가 나오게 된다.

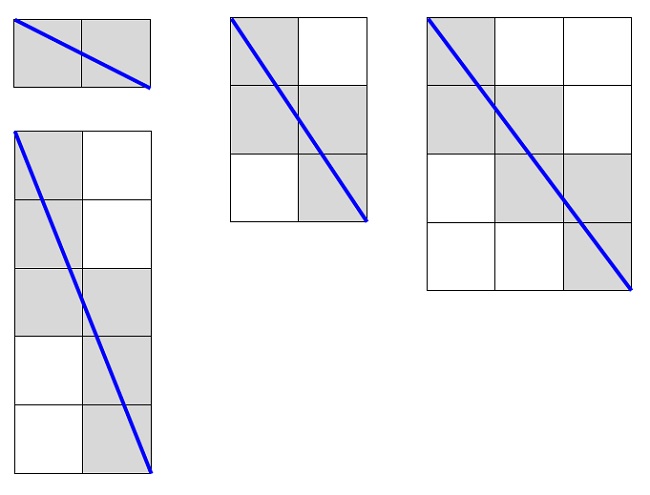
이러한 갯수가 g개 반복되므로 식을 정리하면 \(g * ((w/g) + (h/g) -1) = w + h + g\)가 된다. 전체 갯수인 w x h에서 해당 값을 빼주면 문제 해결.

코드는 math 라이브러리의 gcd 기능을 쓰게되면 보다시피 되게.. 심플하다ㅠ

사용 언어 : Python3

import math

def solution(w,h):
    return w * h - (w + h - math.gcd(w,h))