힙(Heap)에 대해서 알아보자.

위키백과에 따르면 ‘힙(heap)은 최댓값 및 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안된 완전이진트리를 기본으로 한 자료구조’라고 한다. 그렇다. 그냥 규칙있는 완전이진트리라고 생각하면 된다. 아래의 그림 기준으로 왼쪽이 최대 힙이고 오른쪽이 최소 힙이다.

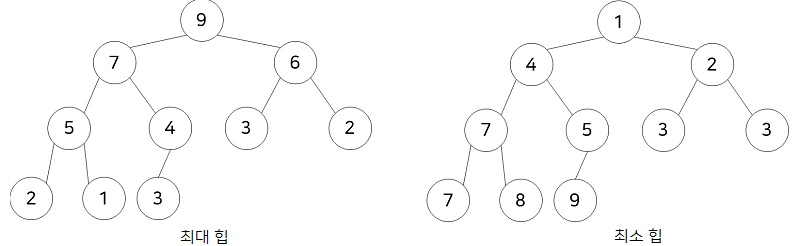
최대 힙의 정의는 부모 노드의 키값이 자식 노드의 키값보다 크거나 같은 완전 이진 트리이다. 즉, Key(부모 노드) >= Key(자식 노드) 여야 하고, 최소 힙은 반대가 된다.

힙(Heap)의 구현 방법

힙은 보통 배열로 구현한다. 완전 이진 트리이므로 각 노드에 번호를 붙일 수 있고, 이 번호를 배열의 인덱스라고 생각하면 구현하기 쉽다.

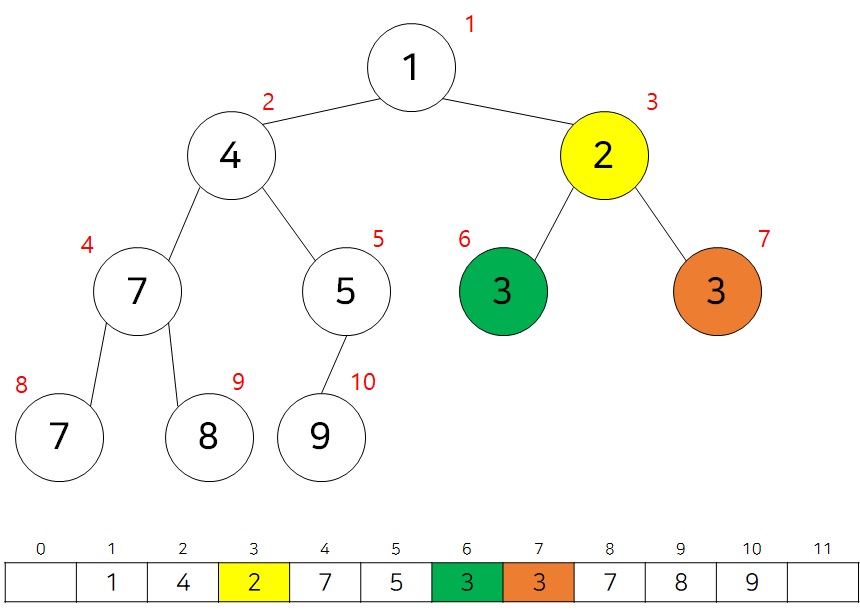
위와 같이 구현하면 아래와 같이 부모 노드와 자식 노드를 찾기 쉬워진다.

• 왼쪽 자식의 인덱스 = (부모의 인덱스) x 2
• 오른쪽 자식의 인덱스 = (부모의 인덱스) x 2 + 1
• 부모의 인덱스 = (자신의 인덱스) / 2

위의 그림에서 노란색 기준으로 생각해보면 쉽다.

• 왼쪽 자식의 인덱스 = (3) x 2 = 6
• 오른쪽 자식의 인덱스 = (3) x 2 + 1 = 7

힙(Heap)의 삽입

힙의 삽입은 능력제 회사(존재한다고 가정)를 떠올리면 된다. 신입사원이 들어오면 먼저 말단에 앉힌 다음에, 능력을 봐서 위로 승진시킨다. (라고 책에 써져있다. ㅋㅋㅋㅋ)

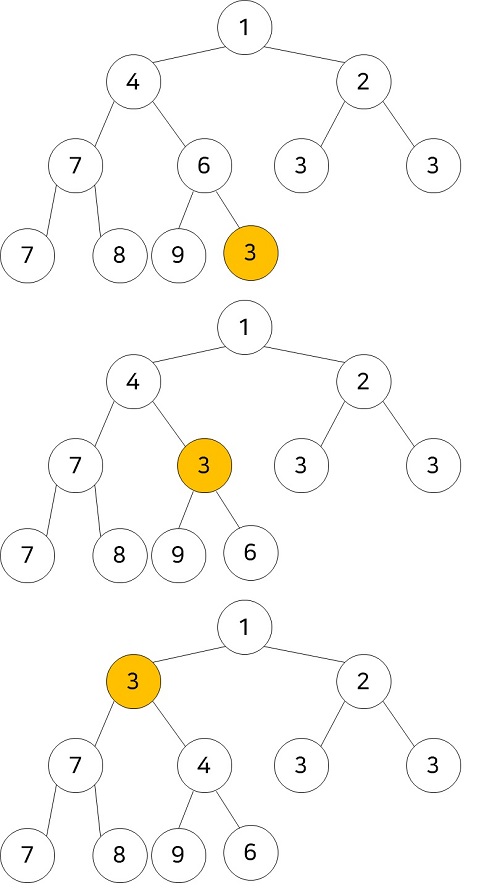
위와 같이 일단 배열의 가장 끝에 넣은 다음에 부모 노드와 비교하면서 하나씩 위로 올려준다.

힙(Heap)의 삭제

힙에서 삭제란 루트 노드를 삭제하는 것을 의미한다. 이 경우에는 힙의 가장 마지막 노드를 루트 노드로 가져와서 자식 노드와 비교하면서 아래로 내려준다. 힙의 삭제를 어떻게 구현하냐에 따라 다르겠지만, 보통 현재 노드의 자식노드중 더 작은 자식노드를 찾아서 바꿔준다.

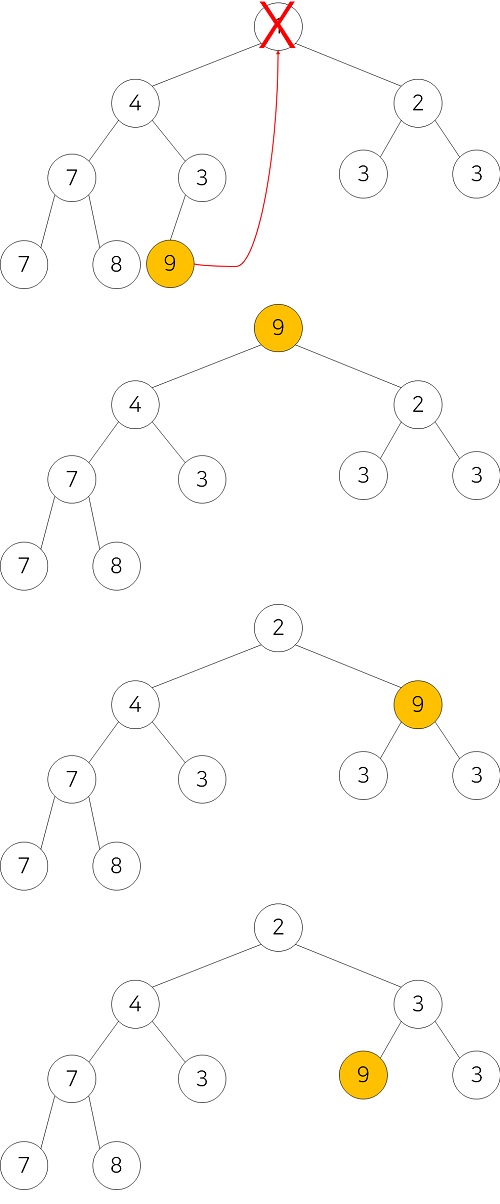
힙(Heap)의 정렬

위에서 얘기한대로 힙 구현, 삭제, 삽입연산까지 모두 구현되었다면, 힙 정렬은 매우 쉽다. 배열을 최소 힙이든 최대 힙이든 힙에 넣어주고 삭제 된 값을 배열에 순차적으로 넣어주면 된다.

그렇다면 이렇게 번거로운 행동을 왜 하느냐. 시간 복잡도가 좋기 때문이다. 즉 효율성 문제에 접근하기 좋다. 흔히 아는 Quick Sort의 경우 평균적으로 시간복잡도는 \(O(NlogN)\)이지만, 최악의 경우 \(O(N^2)\)이 되는 반면에, Heap Sort는 최악의 경우에도 \(O(NlogN)\)을 보장하기 때문이다.